En el año 2020, se estableció un documento en el cual se busca una meta clara: Chile debe ser un país carbono neutral al año 2050.

Para esto, se busca actualizar las medidas para reducir sus emisiones de gases de efecto invernadero y enfrentar los impactos del cambio climático.

En octubre del año 2020, el 61% de la generación eléctrica inyectada en la matriz chilena provenía de energías renovables. De lo anterior, es posible notar que queda un largo camino para llegar a la meta de carbono neutralidad. Se necesitará, por tanto, todo tipo soluciones para ser implementadas en las próximas tres décadas.

En esta misma línea, la energía hidráulica es una gran candidata para utilizarse como fuente de energía limpia. Tiene bajo costo de generación, ya que evita gastos en combustible (por utilizar el agua), y puede reaccionar rápido a fluctuaciones en consumo.

Una muestra de esto en la actualidad, es que en el mes de octubre, la energía renovable más utilizada fue, precisamente, la energía hidráulica, alcanzando un tercio de toda la producción energética del país. Considerando, además, el gran potencial hídrico de Chile, por sus extensas costas y numerosas cuencas, es fundamental educar en el aspecto de la extracción de energía hidráulica a bajo costo y con alta eficiencia. En este proyecto, se detalla un modelo de turbina Savonius para estudiar su comportamiento ante un flujo.

La turbina de Savonius es una turbina de eje vertical que tiene álabes o palas adosadas a su eje. Estas se diseñan para convertir la energía del viento o agua en torque para rotar el eje central. De esta forma, pueden generar energía eléctrica mediante la rotación de una bobina conductora sometida a un campo magnetico.

Esta turbina fue creada en el año 1922 por el ingeniero finés Sigurd Johannes Savonius. No obstante, en Europa se ha experimentando con turbinas similares de eje vertical desde mucho antes.

La turbina de Savonius cuenta con un diseño extremadamente sencillo. Por su forma de “S”, un álabe recibe un mayor arrastre del viento o agua, mientras que la otra paleta ofrece menos resistencia, al exponer su cara convexa.

Si bien la turbina de Savonius es bastante simple, su diseño es relativamente ineficiente, ya que la paleta que gira en contra de la dirección del flujo presenta igualmente una alta resistencia, contrarrestando fuertemente el efecto de la paleta cóncava. Esta ineficiencia se hace más notoria en fluidos más viscosos, como el agua, por lo que su uso se ve disminuido en ese ámbito.

Debido a lo anterior, en la práctica se instalan las turbinas pone en lugares elevados y con vientos muy fuertes. También se ha modificado la forma de sus álabes para que estos aprovechen mejor la energía del viento.

Uno de los parámetros modificables en una turbina de Savonius es el número de álabes. Se pueden superponer varios rotores y modificar el perfil geométrico que posee cada álabe.

Otras variables a tener en consideración son la altura de la turbina, el radio de los álabes y el espacio central entre estos (espacio entre el inicio del álabe y el eje del rotor).

Todas estas variables influyen en mayor o menor medida a la eficiencia de la turbina, y justamente esto es lo que busca visualizar y permitir experimentar nuestro proyecto.

Los parámetros descritos anteriormente se conjugan para definir en el factor de potencia (Cₚ), que es un número adimensional que indica cuánta energía disponible del fluido es extraída. Este se calcula usando la potencia de la turbina (P) la masa específica de la turbina (ρ), su área de la sección transversal de la turbina (A) y la velocidad del flujo (V).

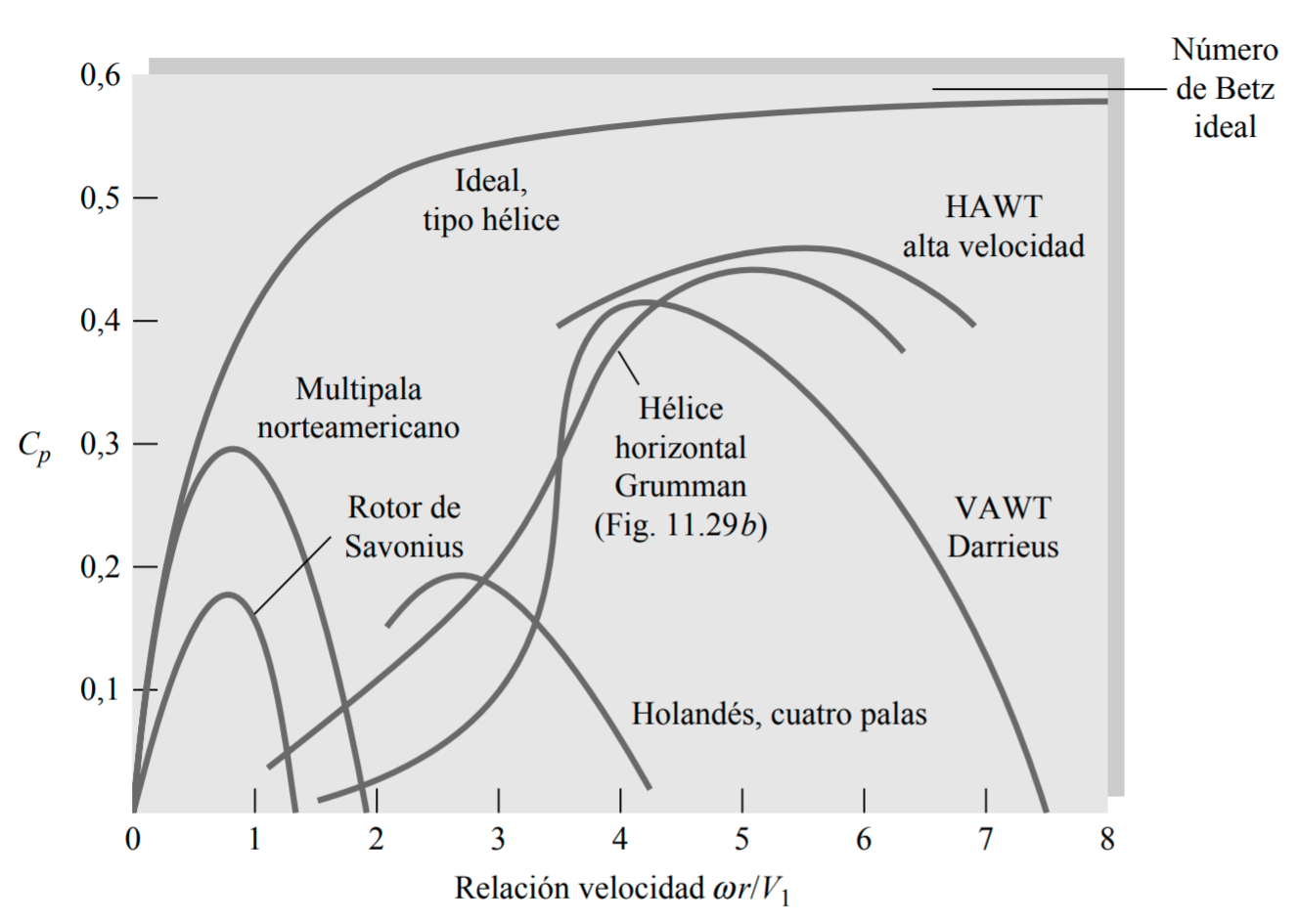
Existe un límite teórico en el factor de potencia, que rige a todas las turbinas imaginables. Es similar al límite de Carnot que aplica en la termodinámica. Este es llamado límite de Betz, y tiene un valor adimensional de 0.593. Las turbinas más eficientes alcanzan 0.8 y hasta 0.9 veces este número, es decir, cerca de un 50% de la energía cinética del fluido es extraíble en la práctica por una turbina. Una explicación simple de este fenómeno es que, si una turbina extrajera toda la energía cinética de una partícula de fluido, entonces esta quedaría estacionaria justo después de pasar por el álabe, con lo cual, la turbina misma no podría moverse, al chocar con una partícula estática de fluido. En otras palabras, para que la turbina pueda rotar, debe existir una velocidad final no nula, por lo que la eficiencia no puede ser 100%.

Para calcular la potencia, es necesario conocer la velocidad angular de la turbina (ω), y el torque (τ), que se calcula usando su radio (R), la velocidad de entrada a la turbina (V₁) y su velocidad de salida (V₂).

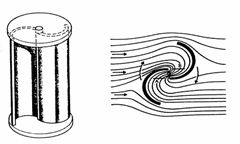
Como se aprecia en el diagrama de esta sección, las turbinas Savonius están en el espectro bajo de la eficiencia, según su coeficiente de potencia Cₚ. Para el caso de turbinas de viento, las de eje horizontal (HAWT: horizontal axis wind turbine), son las que tienen el mejor rendimiento.

Gracias a las tecnologías web de la actualidad, este sitio brinda una aplicación diseñada para un aprendizaje interactivo, con el que se pueda visualizar cómo el cambio de parámetros en la turbina influyen en su rotación, y en el factor de potencia que esta turbina prueba desarrollar.

Para simular el flujo, se utilizan las ecuaciones de Navier Stokes incompresibles. Los parámetros como la velocidad de flujo, cantidad de aspas, radio de separación de las turbinas, entre otros factores están a disposición en el visualizador más abajo.